Answer:
1.

2.
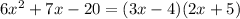
3.
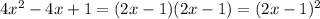
4.
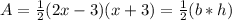
b = 2x-3 and h = x+3.
Explanation:
1. First, we need to find two numbers that multiply together to get -10 and 2x².
For example we chose this combination:
2x² = 2x*x let's define a=2x and b=x
-10 = (-5)*2 let's define c=-5 and d=2
Now we must verify that a*d + b*c = -x (-x is the middle term of the polynomial)
2*2x + (-5)*x = 4x - 5x = -x, so these values are correct.
Then we can rewrite the polynomial as:
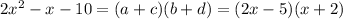
2. We can use the same method.
6x² = 3x*2x let's define a=3x and b=2x
-20 = (-4)*5 let's define c=-4 and d=5
Now we must verify that a*d + b*c = 7x
3x*5 + 2x*(-4) = 15x - 8x = 7x, it is correct!
Then we can rewrite the polynomial as:
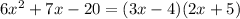
3. Before factoring it, we can multiply by -1 each term, we will have
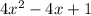
4x² = 2x*2x let's define a = 2x and b = 2x
1 = (-1)*(-1) let's define c = -1 and d = -1
Now we must verify that a*d + b*c = -4x
2x*(-1) + 2x*(-1) = -4x, it is correct!
Then we can rewrite the polynomial as:
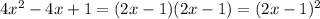
4.

If we factor out 1/2 of each term, we will have:
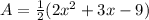
And using the above method we can factorize
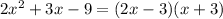
So, the area will be:
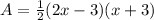
and the area of the triangle is base times height over 2 ((b*h)/2)
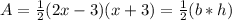
Therefore, b = 2x-3 and h = x+3.
I hope it helps you!