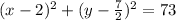Answer:
The standard form of the given circle is
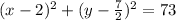
Explanation:
Given that the end points of a diameter of a circle are (6,2) and (-2,5);
Now to find the standard form of the equation of this circle:
The center is (h,k) of the circle is the midpoint of the given diameter
midpoint formula is

Let
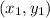 and
and
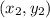 be the given points (6,2) and (-2,5) respectively.
be the given points (6,2) and (-2,5) respectively.


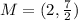
Therefore the center (h,k) is
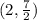
now to find the radius:
The diameter is the distance between the given points (6,2) and (-2,5)
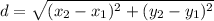
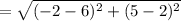
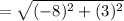
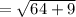
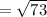
Therefore the radius is
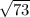
i.e.,
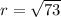
Therefore the standard form of the circle is

Now substituting the center and radiuswe get
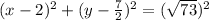
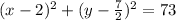
Therefore the standard form of the given circle is