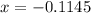Answer:
a)
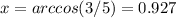
Just one solution
b)
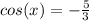
But we know that the cosine can't be negative so then this equation no have solutions on the reals.
c)
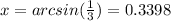
This is only the solution on the interval assumed.
d)
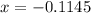
Explanation:
a. 5 cos(x) − 3 = 0
For this case we can do this:

Now we can divide both sides by 5 and we got:

If we apply arccos on both sides we got:
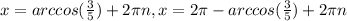
So for this case the possible solution is:
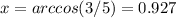
Just one solution. This is only the solution on the interval assumed.
b. 3 cos(x) + 5 = 0
We can do this:
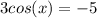
Then we can divide by 3 both sides and we got:
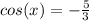
But we know that the cosine can't be negative so then this equation no have solutions on the reals.
c. 3 sin(x) − 1 = 0
We can do this:
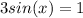
Then we can divide both sides by 3 and we got:
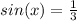
The general solutions would be:
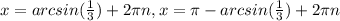
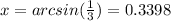
This is only the solution on the interval assumed.
d. tan(x) = −0.115
For this case we can solve the value of x like this:
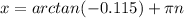
And then the only possible solution for this case is: