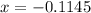Question

Solve each trigonometric equation such that 0 ≤ x ≤ 2????. Round answers to three decimal places.

a. 5 cos(x) − 3 = 0
b. 3 cos(x) + 5 = 0
c. 3 sin(x) − 1 = 0
d. tan(x) = −0.115

Answer 1

a)
`x= arccos(3/5) = 0.927`

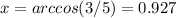
Just one solution

b)
`cos(x) = -(5)/(3)`

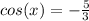
But we know that the cosine can't be negative so then this equation no have solutions on the reals.

c)
`x = arcsin((1)/(3))=0.3398`

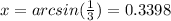
This is only the solution on the interval assumed.

d)
`x= -0.1145`

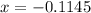
Explanation:

a. 5 cos(x) − 3 = 0

For this case we can do this:

`5 cos(x) = 3`

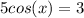
Now we can divide both sides by 5 and we got:

`cos (x) = (3)/(5)`

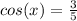
If we apply arccos on both sides we got:

`x = arccos ((3)/(5))+2\pi n, x=2\pi-arccos ((3)/(5))+2\pi n`

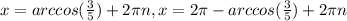
So for this case the possible solution is:

`x= arccos(3/5) = 0.927`

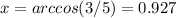
Just one solution. This is only the solution on the interval assumed.

b. 3 cos(x) + 5 = 0

We can do this:

`3 cos (x) = -5`

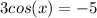
Then we can divide by 3 both sides and we got:

`cos(x) = -(5)/(3)`

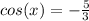
But we know that the cosine can't be negative so then this equation no have solutions on the reals.

c. 3 sin(x) − 1 = 0

We can do this:

`3 sin(x) = 1`

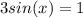
Then we can divide both sides by 3 and we got:

`sin(x) = (1)/(3)`

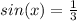
The general solutions would be:

`x = arcsin((1)/(3)) + 2\pi n , x= \pi -arcsin ((1)/(3)) + 2\pi n`

`x = arcsin((1)/(3))=0.3398`

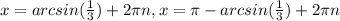
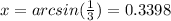
This is only the solution on the interval assumed.

d. tan(x) = −0.115

For this case we can solve the value of x like this:

`x = arctan(-0.115) +\pi n`

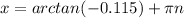
And then the only possible solution for this case is:

`x= -0.1145`