Answer:

Explanation:
For this case since the order matter we can use permutatiosn in order to solve the total number of ways on which we can order the 5 letters on this case we want to select 3 letters. We need to remember that the general formula for permutations is given by :
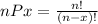
Where n is the total of letters and x the number of letters that we want to select.
For this case we have this for the total of possibilites:
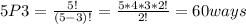
But on this case we need another condition "A and B never come together". So for this case we can put on 6 ways 3 letters with A and B as we can see here:
X on this case represent any letter different from A or B (C,D or E)
AB X
AX B
X AB
BA X
B XA
X BA
Because the order matter on this case 6*3=18 are the total of ways that we can order this because we have 3 possible letters for X (C,D or E). And then the total of ways to select 3 letters where AB can't be together are:
