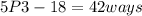Question

In how many ways can 3 letters out of five distinct 5 distinct letters A, B, C, D and E be arranged in a straight line so that A and B never come together?

Answer 1

`5P3 - 18 =42 ways`

Explanation:

For this case since the order matter we can use permutatiosn in order to solve the total number of ways on which we can order the 5 letters on this case we want to select 3 letters. We need to remember that the general formula for permutations is given by :

`nPx = (n!)/((n-x)!)`

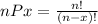
Where n is the total of letters and x the number of letters that we want to select.

For this case we have this for the total of possibilites:

`5P3 = (5!)/((5-3)!)= (5*4*3*2!)/(2!)=60 ways`

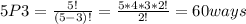
But on this case we need another condition "A and B never come together". So for this case we can put on 6 ways 3 letters with A and B as we can see here:

X on this case represent any letter different from A or B (C,D or E)

AB X

AX B

X AB

BA X

B XA

X BA

Because the order matter on this case 6*3=18 are the total of ways that we can order this because we have 3 possible letters for X (C,D or E). And then the total of ways to select 3 letters where AB can't be together are:

`5P3 - 18 =42 ways`