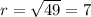Answer:
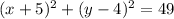
If we compare this equation with the general formula for a circle given by:
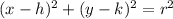
We see that h = -5 and k = 4 so then the center is V = (-5,4). And the radius would be
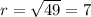
Explanation:
For this case we have the following expression:
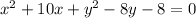
We can complete the squares for this case like this"
![[x^2 +10 x +((10)/(2))^2] + [y^2 -8y +((8)/(2))^2] = 8 +((10)/(2))^2 + ((8)/(2))^2](https://img.qammunity.org/2021/formulas/mathematics/high-school/h3ym5yrzf4p4x1la66lnpmua401j50tdoy.png)
And we can express this like that:

And we can simplify like this:
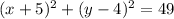
If we compare this equation with the general formula for a circle given by:
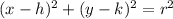
We see that h = -5 and k = 4 so then the center is V = (-5,4). And the radius would be