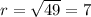Question

The graph of the equation below is a circle. Identify the center and radius of the circle. x^2 + 10x + y^2 − 8y − 8 = 0

Answer 1

`(x+5)^2 + (y-4)^2 = 49`

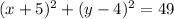
If we compare this equation with the general formula for a circle given by:

`(x-h)^2 +(y-k)^2 = r^2`

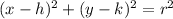
We see that h = -5 and k = 4 so then the center is V = (-5,4). And the radius would be
`r = √(49)= 7`

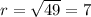
Explanation:

For this case we have the following expression:

`x^2 + 10 x + y^2 -8y -8 =0`

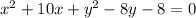
We can complete the squares for this case like this"

`[x^2 +10 x +((10)/(2))^2] + [y^2 -8y +((8)/(2))^2] = 8 +((10)/(2))^2 + ((8)/(2))^2`

And we can express this like that:

`(x^2 +10x + 25) +(y^2 -8y + 16)= 8+ 25+ 16=49`

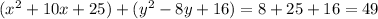
And we can simplify like this:

`(x+5)^2 + (y-4)^2 = 49`

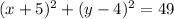
If we compare this equation with the general formula for a circle given by:

`(x-h)^2 +(y-k)^2 = r^2`

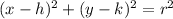
We see that h = -5 and k = 4 so then the center is V = (-5,4). And the radius would be
`r = √(49)= 7`