Question

Use the double-angle formula for cosine to establish the identity cos (theta / 2) = ±cos(theta) + 1 / 2 .

Answer 1

See explanation and proof below.

Explanation:

For this case we want to proof this identity:

`cos((\theta)/(2)) = \pm \sqrt{(1+ cos(x))/(2)}`

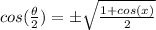
And we need to us the double angle formula given by:

`cos^2 (x) = (1+ cos (2x))/(2)`

If we use a substitution for example
`x = (\theta)/(2)` we see that the double angle formila is given by:

`cos^2((\theta)/(2)) = (1+ cos (2(\theta)/(2)))/(2)`

And we got:

`cos^2((\theta)/(2)) = (1+ cos (\theta))/(2)`

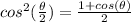
And if we apply sqaure root on both sides we got:

`cos((\theta)/(2)) = \pm \sqrt{(1+ cos (\theta))/(2)}`

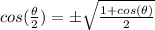
And that complete the proof