Question

If 36 Superscript 12 minus m Baseline = 6 Superscript 2 m, what is the value of m?

Answer 1

vouch, m=6 is correct.

Answer 2

For given equation the value m=6

That is the value of m is 6.

Explanation:

Given equation can be written as

`36^(12-m)=6^(2m)`

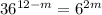
Now to find the value of m in the equation:

`36^(12-m)=6^(2m)`

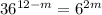
`36^(12).36^(-m)=6^(2m)` ( using
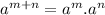`a^(m+n)=a^m.a^n`) Here m=12 and n=-m

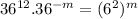`36^(12).36^(-m)=(6^(2))^(m)` (using
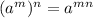`(a^m)^(n)=a^(mn)`) Here m=2 and n=m

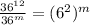`(36^(12))/(36^(m))=(6^(2))^(m)` (using the property
`a^(m-n)=(a^m)/(a^n)` Here m=12 and n=m

`(36^(12))/(36^(m))=36^(m)`

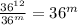
Now multiplying
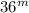`36^(m)` on both sides

`(36^(12))/(36^(m))* 36^(m)=36^(m)* 36^(m)`

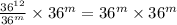
`36^(12)=36^(m+m)` ( using
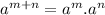`a^(m+n)=a^m.a^n`) Here m=m and n=m

`36^(12)=36^(2m)`

In the above we have base numbers are same so that we can equate the powers of these numbers

12=2m

Rewritting the equation

`2m=12`

`m=(12)/(2)`

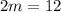
m=6

Therefore the value of m is 6.

For given equation the value m=6.