The solutions for ‘x’ are 2 and -5
Explanation:
Given equation:
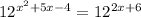
Since the base on both sides as ‘12’ are the same, we can write it as
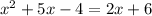
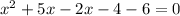
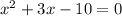
Often, the value of x is easiest to solve by
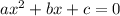 by factoring a square factor, setting each factor to zero, and then isolating each factor. Whereas sometimes the equation is too awkward or doesn't matter at all, or you just don't feel like factoring.
by factoring a square factor, setting each factor to zero, and then isolating each factor. Whereas sometimes the equation is too awkward or doesn't matter at all, or you just don't feel like factoring.
The Quadratic Formula: For
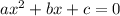 , the values of x which are the solutions of the equation are given by:
, the values of x which are the solutions of the equation are given by:
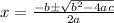
Where, a = 1, b = 3 and c = -10
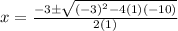
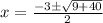
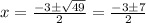
So, the solutions for ‘x’ are
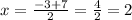
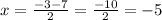
The solutions for ‘x’ are 2 and -5