Question

Which data set has the largest standard deviation

A.3,4,3,4,3,4,3
B.1,6,3,15,4,12,8
C. 20, 21,23,19,19,20,20
D.12,14,13,14,12,13,12

Answer 1

B

Step-by-step explanation:

Answer 2

The data set marked as B has the largest standard deviation

Step-by-step explanation:

Standard Deviation

It's a number used to show how a set of measurements is spread out from the average value. A low standard deviation means that most of the values are close to the average. A high standard deviation means that the numbers are more spread out.

The formula for the standard deviation is

`\displaystyle \sigma=\sqrt{(\sum (x_i-\mu)^2)/(n)}`

Where
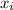`x_i` is the value of each measurement, n is the number of elements in the set, and
`\mu` is the average or media of the values, defined as

`\displaystyle \mu=(\sum x_i)/(n)`

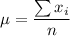
Let's analyze each set of data:

A.3,4,3,4,3,4,3

The average is

`\displaystyle \mu=(3+4+3+4+3+4+3)/(7)=3.43`

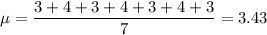
Computing the stardard deviation:

`\sigma=\sqrt{((3-3.43)^2+(4-3.43)^2+(3-3.43)^2+(4-3.43)^2+(3-3.43)^2+(4-3.43)^2+(3-3.43)^2)/(7)}`

`\sigma=0.5`

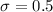
B.1,6,3,15,4,12,8

The average is

`\displaystyle \mu=(1+6+3+15+4+12+8)/(7)=7`

Computing the stardard deviation:

`\sigma=\sqrt{((1-7)^2+(6-7)^2+(3-7)^2+(15-7)^2+(4-7)^2+(12-7)^2+(8-7)^2)/(7)}`

`\sigma=4.7`

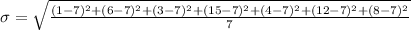
C. 20, 21,23,19,19,20,20

The average is

`\displaystyle \mu=(20+21+23+19+19+20+20)/(7)=20.29`

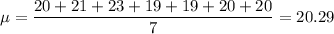
Computing the stardard deviation:

`\sigma=\sqrt{((20-20.29)^2+(21-20.29)^2+(23-20.29)^2+(19-20.29)^2+(19-20.29)^2+(20-20.29)^2+(20-20.29)^2)/(7)}`

`\sigma=1.3`

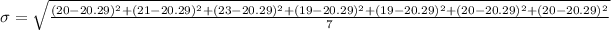
D.12,14,13,14,12,13,12

The average is

`\displaystyle \mu=(12+14+13+14+12+13+12)/(7)=12.86`

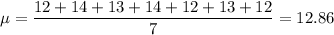
Computing the stardard deviation:

`\sigma=\sqrt{((12-12.86)^2+(14-12.86)^2+(13-12.86)^2+(14-12.86)^2+(12-12.86)^2+(13-12.86)^2+(12-12.86)^2)/(7)}`

`\sigma=0.8`

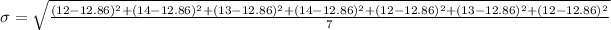
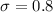
We can see the data set marked as B has the largest standard deviation