Answer:
a.

b.
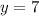
c.
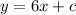
d.
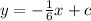
Explanation:
part a: parallel to x = 3
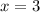 it is a vertical line that passes through
it is a vertical line that passes through
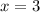 , so a parallel line to this that passes through (-2,7) must be
, so a parallel line to this that passes through (-2,7) must be
 which is also a vertical line (thus they are parallel because they will never touch).
which is also a vertical line (thus they are parallel because they will never touch).
part b: perpendicular to x = -3
 it is a vertical line that passes through
it is a vertical line that passes through
 , so a perpendicular line to this that passes through (-2,7) must be
, so a perpendicular line to this that passes through (-2,7) must be
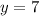 because this is horizontal line, and since one line is vertical and the other is horizontal they are perpendicular.
because this is horizontal line, and since one line is vertical and the other is horizontal they are perpendicular.
part c: parallel to y = 6x - 13
For two lines to be parallel they must have the same slope. The slope of a line is the number that accompanies the x. for
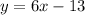 the slope is 6. the equation for a parallel line will be:
the slope is 6. the equation for a parallel line will be:
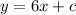 (where c can be any number) because the slope (6) is the same for both.
(where c can be any number) because the slope (6) is the same for both.
part d: perpendicular to y=6x-13
The condition for two lines to be perpendicular is:
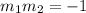
where
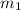 is the slope of one line, and
is the slope of one line, and
 the slope of the perpendicular line. We have the slope of the first line as we found in part c:
the slope of the perpendicular line. We have the slope of the first line as we found in part c:
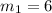 so the slope of the second line has to be:
so the slope of the second line has to be:
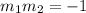
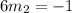
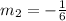
so an equation of a line with a slope of
 can be:
can be:
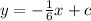 (where c can be any number)
(where c can be any number)