Answer:
We verified that
![a^3+b^3+c^3-3abc=(a+b+c)/(2)[(a-b)^2+(b-c)^2+(c-a)^2]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/47v4t96llbjql5zb10qjmxpvk4prs2afa1.png)
Hence proved
Explanation:
Given equation is
![a^3+b^3+c^3-3abc=(a+b+c)/(2)[(a-b)^2+(b-c)^2+(c-a)^2]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/47v4t96llbjql5zb10qjmxpvk4prs2afa1.png)
We have to prove that
![a^3+b^3+c^3-3abc=(a+b+c)/(2)[(a-b)^2+(b-c)^2+(c-a)^2]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/47v4t96llbjql5zb10qjmxpvk4prs2afa1.png)
That is to prove that LHS=RHS
Now taking RHS
![(a+b+c)/(2)[(a-b)^2+(b-c)^2+(c-a)^2]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/hyh3o732l5kicijdzf6l742m08tpmtsyxz.png)
![=(a+b+c)/(2)[a^2-2ab+b^2+b^2-2bc+c^2+c^2-2ac+a^2]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/c71tgjnnpj3hosywgxzzz9k7s2twb6am26.png) (using
(using
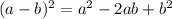 )
)
![=(a+b+c)/(2)[2a^2-2ab+2b^2-2bc+2c^2-2ac]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/rea17veluhxt5pqvfyn17got9dmmgisbm5.png) (adding the like terms)
(adding the like terms)
![=(a+b+c)/(2)[2a^2+2b^2+2c^2-2ab-2bc-2ac]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/gjq7hzvgbqmvuarx0xgotyz3rbi0dwvkus.png)
![=(a+b+c)/(2)* 2[a^2+b^2+c^2-ab-bc-ac]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/w2q31exi5mj33r6kxvbrbp182nvays897o.png)
![=a+b+c[a^2+b^2+c^2-ab-bc-ac]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/nehc7psvf66r41fuqtp9nbcwm7osy352c5.png)
Now multiply the each term to another each term in the factor
![=a^3+ab^2+ac^2-a^2b-abc-a^2c+ba62+b^3+bc^2-ab^2-b^2c-abc+ca^2+cb^2+c^3-abc-bc^2-ac^2]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/dql7hm6hc6q7u64af35wbezdajcejqbyqf.png)
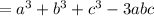 (adding the like terms and other terms getting cancelled)
(adding the like terms and other terms getting cancelled)
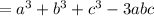 =LHS
=LHS
Therefore LHS=RHS
Therefore
![a^3+b^3+c^3-3abc=(a+b+c)/(2)[(a-b)^2+(b-c)^2+(c-a)^2]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/47v4t96llbjql5zb10qjmxpvk4prs2afa1.png)
Hence proved.