Question

Pls help me.
proove it ^​

Answer 1

We verified that
`a^3+b^3+c^3-3abc=(a+b+c)/(2)[(a-b)^2+(b-c)^2+(c-a)^2]`

Hence proved

Explanation:

Given equation is
`a^3+b^3+c^3-3abc=(a+b+c)/(2)[(a-b)^2+(b-c)^2+(c-a)^2]`

We have to prove that
`a^3+b^3+c^3-3abc=(a+b+c)/(2)[(a-b)^2+(b-c)^2+(c-a)^2]`

That is to prove that LHS=RHS

Now taking RHS

`(a+b+c)/(2)[(a-b)^2+(b-c)^2+(c-a)^2]`

`=(a+b+c)/(2)[a^2-2ab+b^2+b^2-2bc+c^2+c^2-2ac+a^2]` (using
`(a-b)^2=a^2-2ab+b^2`)

`=(a+b+c)/(2)[2a^2-2ab+2b^2-2bc+2c^2-2ac]` (adding the like terms)

`=(a+b+c)/(2)[2a^2+2b^2+2c^2-2ab-2bc-2ac]`

`=(a+b+c)/(2)* 2[a^2+b^2+c^2-ab-bc-ac]`

`=a+b+c[a^2+b^2+c^2-ab-bc-ac]`

Now multiply the each term to another each term in the factor

`=a^3+ab^2+ac^2-a^2b-abc-a^2c+ba62+b^3+bc^2-ab^2-b^2c-abc+ca^2+cb^2+c^3-abc-bc^2-ac^2]`

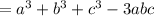`=a^3+b^3+c^3-3abc` (adding the like terms and other terms getting cancelled)

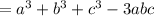`=a^3+b^3+c^3-3abc` =LHS

Therefore LHS=RHS

Therefore
`a^3+b^3+c^3-3abc=(a+b+c)/(2)[(a-b)^2+(b-c)^2+(c-a)^2]`

Hence proved.