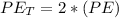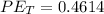Question

The soles of a popular make of running shoe have a force constant of 2.0×105 N/m . Treat the soles as ideal springs for the following questions.

Part A: If a 62 kg person stands in a pair of these shoes, with her weight distributed equally on both feet, how much does she compress the soles?
Part B: How much energy is stored in the soles of her shoes when she's standing?

Answer 1

To solve this problem we will apply the concepts related to Newton's second law with which we will find the weight of the person. We will proceed to apply Hook's law with which we can relate this expression to weight and thus find the displacement. Finally we will apply the elastic potential energy theorem with which we will find the total energy on the shoes.

The weight of the person is

`W = mg\\W =(62)(9.8)\\W = 607.6N`

From the Hook's law

`F= kx`

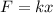
Where,

k = Spring constant

x = Displacement

PART A)

When the person is standing on the shoes that is on spring, the weight of the person equally distributes on both legs therefore the half of the weight of the person is equal to the restoring force in the spring.

`(W)/(2) = kx`

`x = (W)/(2x)`

`x = (607.6)/(2*(2*10^5))`

`x = 0.001519m`

`x = 1.5mm`

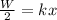
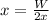
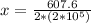
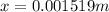
PART B) The potential energy stored in soles of one of the shoes is

`PE = (1)/(2) kx^2`

`PE = (1)/(2) (2*10^5)(0.001519)^2`

`PE = 0.2307J`

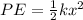
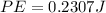
The total energy stored in two shoes would be

`PE_T = 2*(PE)`

`PE_T = 2* (0.2307)`

`PE_T = 0.4614`