Question

To see if the slopes are the same, write an equation setting the two fractions equal to each other. Is this equation true? Why or why not? What does that mean about the slope between points E and A and the slope between the points A and C?

Answer 1

`Slope(EA)=Slope(AC)=(2)/(3)`....Equation is True

Slopes are EQUAL for

1. SAME Line

Hence, E-A-C is the same Line.

Explanation:

Given:

The three points for the given line are

point E( x₁ , y₁) ≡ ( -6 ,-4)

point A( x₂ , y₂) ≡ (0 , 0) .....Origin

point C(x₃ , y₃ ) ≡ (3 , 2)

To Find:

Slope EA = ?

Slope AC = ?

Solution:

For Two point Slope is given as

`Slope=(y_(2)-y_(1) )/(x_(2)-x_(1) )`

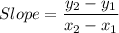
Substituting the values we get

`Slope(EA)=(0--4)/(0--6)=(4)/(6)=(2)/(3)`

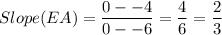
Similarly For AC we have,

`Slope(AC)=(2-0)/(3-0)=(2)/(3)`

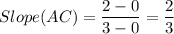
Therefore,

`Slope(EA)=Slope(AC)`....Equation is True

Slopes are EQUAL for

1. Line is Parallel
2. SAME Line

Hence, E-A-C is the same Line.