Question

Which expression is equivalent to the following complex fraction?

Answer 1

B

Explanation:

edg2021

Answer 2

B

Explanation:

Simplify the numerator and denominator of the fraction, that is

`(2)/(x)` -
`(4)/(y)`

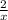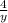
Multiply the numerator/denominator of the first fraction by y

Multiply the numerator/denominator of the second fraction by x

`(2y)/(xy)` -
`(4x)/(xy)`

=
`(2y-4x)/(xy)`

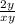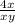
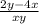
Similarly

`(-5)/(y)` +
`(3)/(x)`

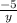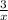
Multiply numerator/denominator of the first fraction by x

Multiply numerator/denominator of second fraction by y

`(-5x)/(xy)` +
`(3y)/(xy)`

=
`(3y-5x)/(xy)`

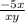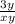
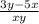
To perform the division

leave the fraction on the numerator

Change division to multiplication

Turn the fraction on the denominator upside down, thus

`(2y-4x)/(xy)` ×
`(xy)/(3y-5x)`

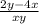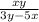
Cancel xy on the numerator and denominator

=
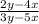`(2y-4x)/(3y-5x)` ← factor 2 out of each term on the numerator

=
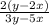`(2(y-2x))/(3y-5x)` → B