Answer:
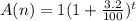
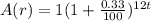
The value of the ring is increasing at a faster rate.
Explanation:
It is given that the value of a necklace increases by 3.2% per year.
Therefore, the value of the necklace after t years will be
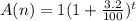 .......... (1)
.......... (1)
{The initial value is given to be $1}
Again, the value of a ring increases by 0.33% per month.
Therefore, the value of the ring after t years will be
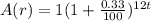 ............ (2)
............ (2)
{The initial value is given to be $1}
Therefore, from equation (1) the value of the necklace after 1 year will be
A(n) = $1.032
And from equation (2) the value of the ring after 1 year will be
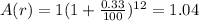 dollars.
dollars.
Therefore, the ring will value more after 1 year.
Therefore, the value of the ring is increasing at a faster rate. (Answer)