Question

Cami is comparing the growth rates in the value of two items in a collection. the value of a necklace increases by 3.2% per year. the value of a ring increases by 0.33% per month. write a function to represent the value of A of the necklace after t years, assuming the inital value of $1 then write an equivalent function with a power of 12t

B. which item is increasing in value at a faster rate? explain
function;
equivalent function;

Answer 1

A(t) = 1.032^t

Ring

Explanation:

A(t) = (1 + 3.2%)^t

A(t) = (1.032)^t

Ring:

(1 + 0.33%)^(12t)

(1 + 0.0033)^(12t)

(1.0033¹²)^t

1.040326705^t

Faster rate: ring

Answer 2

`A(n) = 1(1 + (3.2)/(100))^(t)`

`A(r) = 1(1 + (0.33)/(100) )^(12t)`

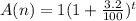
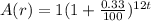
The value of the ring is increasing at a faster rate.

Explanation:

It is given that the value of a necklace increases by 3.2% per year.

Therefore, the value of the necklace after t years will be

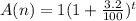`A(n) = 1(1 + (3.2)/(100))^(t)` .......... (1)

{The initial value is given to be $1}

Again, the value of a ring increases by 0.33% per month.

Therefore, the value of the ring after t years will be

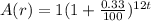`A(r) = 1(1 + (0.33)/(100) )^(12t)` ............ (2)

{The initial value is given to be $1}

Therefore, from equation (1) the value of the necklace after 1 year will be

A(n) = $1.032

And from equation (2) the value of the ring after 1 year will be

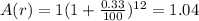`A(r) = 1(1 + (0.33)/(100) )^(12) = 1.04` dollars.

Therefore, the ring will value more after 1 year.

Therefore, the value of the ring is increasing at a faster rate. (Answer)