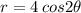Answer:
See below for answers and explanations
Explanation:
Problem 1
- The equation for a rose curve in polar form is either
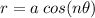 if the pole is horizontal or
if the pole is horizontal or
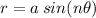 if the pole is vertical.
if the pole is vertical. - The value
 represents the length of each petal
represents the length of each petal
- If
 is odd, there will be
is odd, there will be
 petals
petals - If
 is even, there will be
is even, there will be
 petals
petals
Looking at the graph, the pole is vertical, which means that our polar curve will take the form of
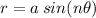 . We see that there are 12 petals, so this must mean that
. We see that there are 12 petals, so this must mean that
 . Additionally, the length of each petal is 4 units, so
. Additionally, the length of each petal is 4 units, so
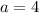 . This means our equation is
. This means our equation is
 , making B the correct answer.
, making B the correct answer.
Problem 2
This polar curve is a limaçon:
- A limaçon is in the form of either
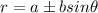 or
or
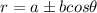 , depending on the direction of the pole where
, depending on the direction of the pole where
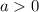 and
and
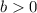
- If
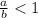 , the limaçon is an inner loop limaçon
, the limaçon is an inner loop limaçon - If
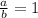 , the limaçon is a cardioid
, the limaçon is a cardioid - If
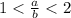 , the limaçon is dimpled with no inner loop
, the limaçon is dimpled with no inner loop - If
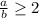 , the limaçon will be convex with no dimple and no inner loop
, the limaçon will be convex with no dimple and no inner loop
Given that our graph is a cardioid (heart-shaped) and it has a vertical pole, this means that our equation takes the form of
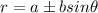 where
where
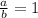 . However, none of the answers look correct
. However, none of the answers look correct
Problem 3
Only
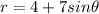 is correct since it takes the form of
is correct since it takes the form of
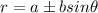
Problem 4
The loop starts at
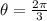 if you look at this on a polar graph and ends at
if you look at this on a polar graph and ends at
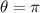 , so this means that
, so this means that
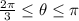 is the correct answer
is the correct answer
Problem 5
We could graph all the points, but the more important points to notice are
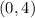 ,
,
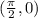 , and
, and
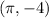 . These show us the petals of the curve, which happens to be the option in the picture. This exact function is
. These show us the petals of the curve, which happens to be the option in the picture. This exact function is