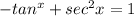 is proved
is proved
Solution:
We have to prove that,
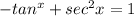
By the trignometric identity,
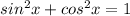
Divide both the sides by
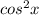 in above identity,
in above identity,
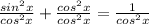 --- eqn 1
--- eqn 1
We know that by definition of tan,
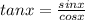
Therefore,
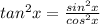
Apply the above in eqn 1
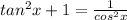 ---- eqn 2
---- eqn 2
By definition of cosine,
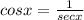
Therefore,
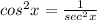
Apply the above in eqn 2
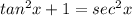
On rewriting we get,
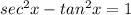
Thus the given identity is proved step by step