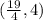Question

Point A is located at (3,6) and point B is located at (10, -2) What are the coordinates of the point that partitions the directed line segment AB in a 1:3 ratio?​

Answer 1

The coordinates of point P is
`((19)/(4) ,4)`

Explanation:

Here, the coordinates of the point A and B are given as:

A (3,6) and B(10,-2)

Let us assume the point P (a,b) divides the line segment AB in ratio 1:3.

Now, by SECTION FORMULA:

The coordinate of the point (a,b) which divides the line segment with points (x1,y1) and (x2,y2) in ratio m1 : m2 is given as:

`(a,b) = ((m_2x_1 + m_1x_2)/(m_1+m_2), (m_2y_1 + m_1y_2)/(m_1+m_2))`

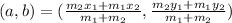
Now, here putting the values of the points A and B as (3,6) and (10,-2) adn ratio m1 : m2 as 1:3, we get:

`(a,b) = ((3(3) + 1(10))/(1+3), (3(6) + 1(-2))/(1+3))\\\implies (a,b)= ((9+10)/(4) , (18-2)/(4))  =((19)/(4) ,(16)/(4) )\\\implies (a,b) = ((19)/(4) ,4 )`

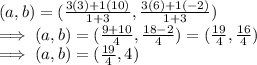
Hence, the coordinates of point P is
`((19)/(4) ,4)`