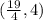Answer:
The coordinates of point P is
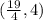
Explanation:
Here, the coordinates of the point A and B are given as:
A (3,6) and B(10,-2)
Let us assume the point P (a,b) divides the line segment AB in ratio 1:3.
Now, by SECTION FORMULA:
The coordinate of the point (a,b) which divides the line segment with points (x1,y1) and (x2,y2) in ratio m1 : m2 is given as:
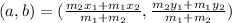
Now, here putting the values of the points A and B as (3,6) and (10,-2) adn ratio m1 : m2 as 1:3, we get:
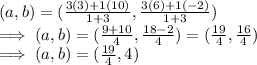
Hence, the coordinates of point P is