Question

A rectangle is inscribed in a circle of radius r. If the rectangle is not a square, which of the following could be the perimeter of the rectangle?

A. 2r3â2r3
B. 2r(3â+1)2r(3+1)
C. 4r2â4r2
D. 4r3â4r3
E. 4r(3â+1)

Answer 1

`2r(√(3)+1)`

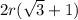
Explanation:

A rectangle is inscribed in a circle of radius r.

Radius of the circle is 'r' . the diameter of circle is 2 times radius is 2r

The diameter of the circle becomes the diagonal of the rectangle.

The one part of the rectangle forms a triangle with hypotenuse 2r

Triangle is a special 30:60:90 degree angle

the ratio of the special triangle is
`1: √(3) :2`

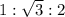
Hypotenuse is '2r' , so the ratio becomes

`r: √(3)r :2r`

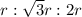
So the width of the rectangle is 'r' and length of the rectangle is
`√(3)r`

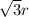
Perimeter = 2 times length + 2 times width

`perimeter = 2√(3) r+2r=2r(√(3)+1)`