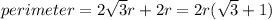Answer:
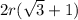
Explanation:
A rectangle is inscribed in a circle of radius r.
Radius of the circle is 'r' . the diameter of circle is 2 times radius is 2r
The diameter of the circle becomes the diagonal of the rectangle.
The one part of the rectangle forms a triangle with hypotenuse 2r
Triangle is a special 30:60:90 degree angle
the ratio of the special triangle is
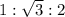
Hypotenuse is '2r' , so the ratio becomes
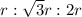
So the width of the rectangle is 'r' and length of the rectangle is
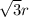
Perimeter = 2 times length + 2 times width