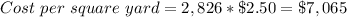Answer:
1. Radius: 30 yards
2. Cost per square yard: $7,065
Explanation:
The formula to find the area of quarter circle is:
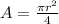
Where "r" is the radius.
Solving for "r":
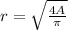
1. Find the area of the playground with the formula for calculate the area of a square:
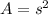
Where "s" is the side lenght.
Since:
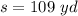
You get:
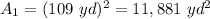
All the skating rings are equal.
So, knowing that the area of the remaining field is:
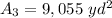
The sum of the areas of all the quarter circles is:
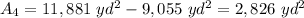
To find the area of each skating ring, divide that result by 4:
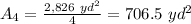
Then, the radius is:

2. Mulitply the total area of the skating rings by $2.50 in order to find the cost of cementing the skating rings per square yard: