Answer:
See proof below
Explanation:
Let
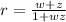 . If w=-z, then r=0 and r is real. Suppose that w≠-z, that is, r≠0.
. If w=-z, then r=0 and r is real. Suppose that w≠-z, that is, r≠0.
Remember this useful identity: if x is a complex number then
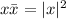 where
where
 is the conjugate of x.
is the conjugate of x.
Now, using the properties of the conjugate (the conjugate of the sum(product) of two numbers is the sum(product) of the conjugates):

=
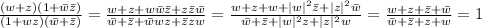
Thus
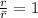 . From this,
. From this,
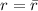 . A complex number is real if and only if it is equal to its conjugate, therefore r is real.
. A complex number is real if and only if it is equal to its conjugate, therefore r is real.