Question 1
1. The reciprocal of 5 plus the reciprocal of 7 is the reciprocal of what number?
Answer:
The reciprocal of 5 plus the reciprocal of 7 is the reciprocal of

Solution:
1. The reciprocal of 5 plus the reciprocal of 7 is the reciprocal of what number?
From given question,

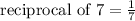
Given that,
reciprocal of 5 + reciprocal of 7 = ?
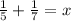
On cross-multiplying we get,
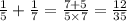
Thus reciprocal is
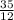
So the reciprocal of 5 plus the reciprocal of 7 is the reciprocal of

Question 2
2. The reciprocal of the product of two consecutive integers is 1/72
Answer:
The value of two consecutive numbers are 8 and 9
Solution:
Let the two consecutive integers be x and x + 1
Given that reciprocal of product of two consecutive integers is
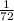
product of two consecutive integers = x(x + 1) =
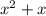
reciprocal of the product of two consecutive integers =
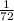
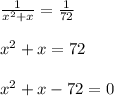
Solve the above quadratic equation by grouping method
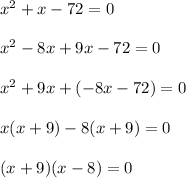
Thus x = -9 or 8
Ignoring negative value,
x = 8
Thus two consecutive integers are x = 8 and x + 1 = 8 + 1 = 9
8 and 9 are two consecutive integers