Answer:
The recoil velocity vector of the cannon is
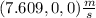
Step-by-step explanation:
We can solve this problem by applying the Momentum Conservation Principle.
The principle of conservation of momentum states that when you have an isolated system with no external forces, we can use the following equation to calculate the final velocity of one object.
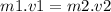 (I)
(I)
Where ''
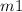 '' and ''
'' and ''
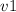 '' are the mass and velocity of the first object.
'' are the mass and velocity of the first object.
And where ''
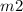 '' and ''
'' and ''
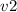 '' are the mass and velocity of the second object.
'' are the mass and velocity of the second object.
The momentum is a vectorial magnitude.
If we use the equation (I) with the data given :
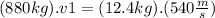
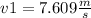
If we considered as negative the sense of the velocity vector from the cannonball, the cannon's velocity vector will have the same direction but opposite sense that the cannonball's velocity vector (It will be positive).
We can give it a vectorial character like this :
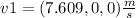
The velocity vector will be entirely in the x-axis.