2 Answers

Adam Spicer · Answer 1 · 2021-09-13T05:37:57+0000

135 cubes are required to fill the prism

Solution:

Given that a rectangular prism with volume of 5 cubic units is filled with cubes with side lengths of
(1)/(3) units

Then the number of cubes required to fill the prism will be given by:

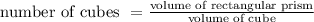
$\text { number of cubes }=\frac{\text {volume of rectangular prism}}{\text {volume of cube}}$

Volume of rectangular prism = 5 cubic units

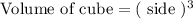
$\text{ Volume of cube}=(\text { side })^(3)$$

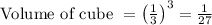
$\text { Volume of cube }=\left((1)/(3)\right)^(3)=(1)/(27)$

Therefore number of cubes required to fill the prism are:

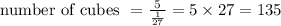
$\text { number of cubes }=(5)/((1)/(27))=5 * 27=135$

Therefore 135 cubes are required to fill the prism

Please log in or register to add a comment.