135 cubes are required to fill the prism
Solution:
Given that a rectangular prism with volume of 5 cubic units is filled with cubes with side lengths of
 units
units
Then the number of cubes required to fill the prism will be given by:
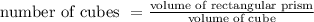
Volume of rectangular prism = 5 cubic units
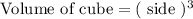

Therefore number of cubes required to fill the prism are:
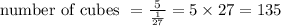
Therefore 135 cubes are required to fill the prism