Question

A rectangular prism with a volume of 555 cubic units is filled with cubes with side lengths of \dfrac13

3
1
​
start fraction, 1, divided by, 3, end fraction unit.
How many \dfrac13
3
1
​
start fraction, 1, divided by, 3, end fraction unit cubes does it take to fill the prism?

Answer 1

135

Explanation:

Answer 2

135 cubes are required to fill the prism

Solution:

Given that a rectangular prism with volume of 5 cubic units is filled with cubes with side lengths of
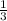`(1)/(3)` units

Then the number of cubes required to fill the prism will be given by:

`\text { number of cubes }=\frac{\text {volume of rectangular prism}}{\text {volume of cube}}`

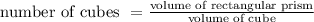
Volume of rectangular prism = 5 cubic units

`\text{ Volume of cube}=(\text { side })^(3)$`

`\text { Volume of cube }=\left((1)/(3)\right)^(3)=(1)/(27)`

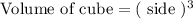
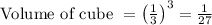
Therefore number of cubes required to fill the prism are:

`\text { number of cubes }=(5)/((1)/(27))=5 * 27=135`

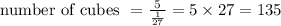
Therefore 135 cubes are required to fill the prism