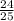Answer:
-
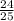
Explanation:
Given 630 < A > 720 then A is in the fourth quadrant where
cosA > 0 and sinA < 0
Given
cosA =
 =
=

Then the triangle is a 3- 4 - 5 with opposite side 4, thus
sinA = -
 = -
= -
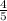
Using the trigonometric identity
sin2A = 2sinAcosA
= 2 × -
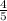 ×
×

=
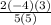 = -
= -