Question

The height in feet of a rocket after t seconds is given by h(t) = 160t - 16t^2.

Find the maximum height the rocket attains in feet​

Answer 1

Explanation:

h(t)=160t-16t^2=-16(t²-10t+25-25)

=-16(t-5)²+400

max. height reached=400 ft

Answer 2

The maximum height 400 feet is attained at t = 5 seconds.

Explanation:

All powers of
`t` in the equation for
`h(t)` are integers that are greater than or equal to zero. Additionally, the greatest power of
`t` is two. Hence,
`h(t)` is a quadratic equation about
`t`.

• Let
  `a` be the coefficient of the
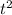  `t^2` term, and
• Let
  `b` be the coefficient of the
  `t` term.

In this case,

• 
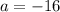  `a = -16`, and
• 
  `b = 160`.

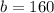The question is asking for the maximum value of this equation. Start by finding the
`t` (time) that would maximize the value of the polynomial.

The graph of a quadratic equation looks like a parabola. Additionally, since the coefficient of
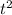`t^2` is less than zero, the parabola opens downward. The maximum value of the parabola would be at its vertex. Additionally, at the vertex,

`\displaystyle t = -(b)/(2a) = -(160)/(2 * (-16)) = (160)/(32) = 5`.

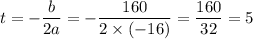In other words, the rocket is at its maximum height when time is equal to 5 seconds.

To find that height, let
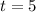`t = 5` and evaluate
`h(t) = 160 \, t - 16\, t^2`:

`160\, t - 16\, t^2 = 160 * 5 - 16 * 5^2 = 400`.

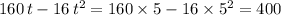That is: the maximum height of the rocket would be 400 feet.