Question

Plz hurry!!!! thank you!!!!

Answer 1

`\mathbf{m\angle A = sin^(-1)((1)/(3)) \approx 19.47^(\circ)}`

Explanation:

This question involves some basic knowledge of trigonometric function. The following formula only works for right angled triangles.

`\mathbf{sin(x) = (perpendicular)/(hypotenuse)}`

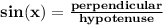
In ΔAKO,

m∠AKO = 90°

Therefore ΔAKO is a right angled triangle. If we take ∠A into consideration then base will be AK, perpendicular will be OK and hypotenuse will be AO.

AO = 15

OK = 5

`\therefore \mathrm{sin(\angle A) = (OK)/(AO) = (5)/(15) = (1)/(3)}`

`\mathrm{sin(\angle A)=(1)/(3)}`

`\mathrm{\angle A=sin^(-1)((1)/(3))}`

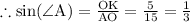
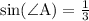
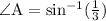
To calculate
`\mathrm{sin^(-1)((1)/(3))}` use scientific calculator

value of
`\mathrm{sin^(-1)((1)/(3))}` is approximately equal to 19.47°

Therefore
`\mathbf{m\angle A \approx 19.47}`

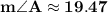
(NOTE : When a line passing through center of a circle, is drawn to a tangent at the point of tangency then the angle made between then is 90°

Therefore m∠AKO = 90°)

Answer 2

∠A ≈ 19.47°

Explanation:

As you know , the angle that tangent makes with the radius at the point of tangency is 90°.

∴∠OKA = 90°

As AO = 15 and OK = 5 ,

`sin(A) = (OK)/(AO)`

`sin(A) = (5)/(15)`

`sin(A) = (1)/(3)`

∠A =
`sin^(-1) ((1)/(3) )`

∠A ≈ 19.47°