f(x) = 7 is a even function
Solution:
Given that we have to find the even function
A function is even if and only if f(–x) = f(x)
Steps to follow:
Replace x with -x and compare the result to f(x). If f(-x) = f(x), the function is even.
If f(-x) = - f(x), the function is odd.
If f(-x) ≠ f(x) and f(-x) ≠ -f(x), the function is neither even nor odd.
Option 1
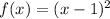
Substitute x = -x in above function
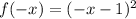
Thus
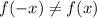
So this is not a even function
Option 2
f(x) = 8x
Substitute x = -x in above function
f(-x) = 8(-x) = -8x
Thus
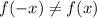
So this is not a even function
Option 3
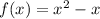
Substitute x = -x in above function
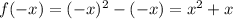
Thus
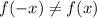
So this is not a even function
Option 4
f(x) = 7
f(-x) = 7
Thus f(-x) = f(x)
Thus it is a even function