Question

Which of the following is an even function

Answer 1

A

Explanation:

edg verified

Answer 2

f(x) = 7 is a even function

Solution:

Given that we have to find the even function

A function is even if and only if f(–x) = f(x)

Steps to follow:

Replace x with -x and compare the result to f(x). If f(-x) = f(x), the function is even.

If f(-x) = - f(x), the function is odd.

If f(-x) ≠ f(x) and f(-x) ≠ -f(x), the function is neither even nor odd.

Option 1

`f(x) = (x - 1)^2`

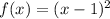
Substitute x = -x in above function

`f(-x) = (-x - 1)^2`

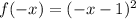
Thus
`f(-x) \\eq f(x)`

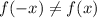
So this is not a even function

Option 2

f(x) = 8x

Substitute x = -x in above function

f(-x) = 8(-x) = -8x

Thus
`f(-x) \\eq f(x)`

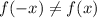
So this is not a even function

Option 3

`f(x) = x^2 - x`

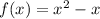
Substitute x = -x in above function

`f(-x) = (-x)^2 - (-x) = x^2 + x`

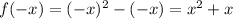
Thus
`f(-x) \\eq f(x)`

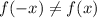
So this is not a even function

Option 4

f(x) = 7

f(-x) = 7

Thus f(-x) = f(x)

Thus it is a even function