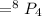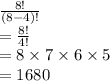Question

How many possible 4-digit combinations are there with the numbers 2, 3, 4, 5, 6, 7, 8, and 9 if none of the numbers appear more than once (i.E. 2343, 2333, 2323, etc.)?

Answer 1

`1680`

Explanation:

we need a 4-digit number from the numbers
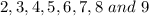`2,3,4,5,6,7,8\ and\ 9` (without repetition ).

possible number at thousand place
`=8`

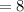
Possible numbers at hundred place
`=8-1=7`

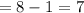
Possible numbers at
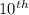`10^(th)` place
`=7-1=6`

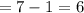
possible number at unit place
`=6-1=5`

So total possible numbers

`=8*7*6*5\\=1680`

Other method :

We are taking
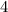`4` numbers out of
`8` and here order matters so we will use permutation.

Total possible numbers
`=^8P_(4)`

`(8!)/((8-4)!)\\ =(8!)/(4!)\\ =8*7*6*5\\=1680`