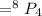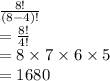Answer:
Explanation:
we need a 4-digit number from the numbers
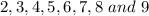 (without repetition ).
(without repetition ).
possible number at thousand place
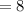
Possible numbers at hundred place
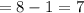
Possible numbers at
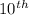 place
place
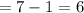
possible number at unit place
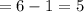
So total possible numbers
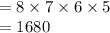
Other method :
We are taking
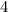 numbers out of
numbers out of
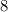 and here order matters so we will use permutation.
and here order matters so we will use permutation.
Total possible numbers