Answer:
Option D. is the correct option.
Explanation:
In this question expression that represents the kth term of a certain sequence is not written properly.
The expression is
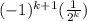 .
.
We have to find the sum of first 10 terms of the infinite sequence represented by the expression given as
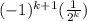 .
.
where k is from 1 to 10.
By the given expression sequence will be
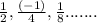
In this sequence first term "a" =

and common ratio in each successive term to the previous term is 'r' =
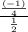
r =
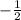
Since the sequence is infinite and the formula to calculate the sum is represented by
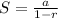 [Here r is less than 1]
[Here r is less than 1]
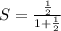
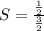
S =

Now we are sure that the sum of infinite terms is
 .
.
Therefore, sum of 10 terms will not exceed

Now sum of first two terms =

Now we are sure that sum of first 10 terms lie between
 and
and

Since
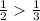
Therefore, Sum of first 10 terms will lie between
 and
and
 .
.
Option D will be the answer.