Question

Consider the following function. Without finding the​ inverse, evaluate the derivative of the inverse at the given point. f(x)=ln(8x+e); (1,0)

Answer 1

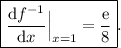
We can use the inverse function derivative theorem:

`\frac{\textrm{d}f^(-1)}{\textrm{d}x}\Big\vert_(x=a) = \frac{1}{\frac{\textrm{d}f}{\textrm{d}x}\Big\vert_(x=f^(-1)(a))}.`

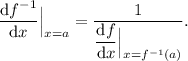
In this case, we want to evaluate
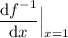`\frac{\textrm{d}f^(-1)}{\textrm{d}x}\Big\vert_(x=1)`, so:

`\frac{\textrm{d}f^(-1)}{\textrm{d}x}\Big\vert_(x=1) = \frac{1}{\frac{\textrm{d}f}{\textrm{d}x}\Big\vert_(x=f^(-1)(1))}.`

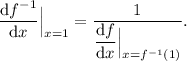
The derivative is:

`\frac{\textrm{d}f}{\textrm{d}x} = \frac{\textrm{d}}{\textrm{d}x}\left[\ln(8x + \textrm{e})\right] = \frac{1}{8x+\textrm{e}}\frac{\textrm{d}}{\textrm{d}x}\left(8x + \textrm{e}\right) = \frac{8}{8x+\textrm{e}}.`

The ordinate of the point is
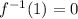`f^(-1)(1) = 0`, so we evaluate:

`\frac{\textrm{d}f}{\textrm{d}x}\Big\vert_(x=0) = \frac{8}{8 * 0+\textrm{e}} = \frac{8}{\textrm{e}}.`

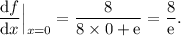
Finally:

`\frac{\textrm{d}f^(-1)}{\textrm{d}x}\Big\vert_(x=1) = \frac{1}{\frac{\textrm{d}f}{\textrm{d}x}\Big\vert_(x=f^(-1)(1))} = \frac{1}{\frac{\textrm{d}f}{\textrm{d}x}\Big\vert_(x=0)} = \frac{1}{\frac{8}{\textrm{e}}} = \frac{\textrm{e}}{8}.`

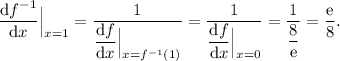
We can check the answer by finding the inverse:

`y = \ln(8x + \textrm{e}) \implies \textrm{e}^y = 8x + \textrm{e} \iff \textrm{e}^y - \textrm{e} = 8x \iff x = \frac{\textrm{e}^y-\textrm{e}}{8},`

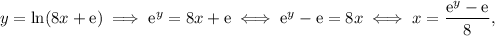
so that

`f^(-1)(x) = \frac{\textrm{e}^x-\textrm{e}}{8}.`

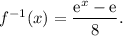
Therefore:

`\frac{\textrm{d}f^(-1)}{\textrm{d}x} = \frac{\textrm{e}^x}{8}.`

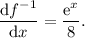
Which finally gives the same answer as before:

`\frac{\textrm{d}f^(-1)}{\textrm{d}x}\Big\vert_(x=1) = \frac{\textrm{e}^1}{8} = \frac{\textrm{e}}{8}.`

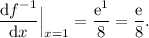
Answer:
`\boxed{\frac{\textrm{d}f^(-1)}{\textrm{d}x}\Big\vert_(x=1) = \frac{\textrm{e}}{8}}.`