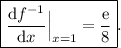
We can use the inverse function derivative theorem:
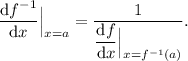
In this case, we want to evaluate
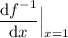 , so:
, so:
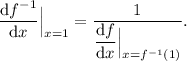
The derivative is:
![\frac{\textrm{d}f}{\textrm{d}x} = \frac{\textrm{d}}{\textrm{d}x}\left[\ln(8x + \textrm{e})\right] = \frac{1}{8x+\textrm{e}}\frac{\textrm{d}}{\textrm{d}x}\left(8x + \textrm{e}\right) = \frac{8}{8x+\textrm{e}}.](https://img.qammunity.org/2021/formulas/mathematics/college/grh9afxtnk7ojuyz37hoxryei9bb73kyol.png)
The ordinate of the point is
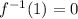 , so we evaluate:
, so we evaluate:
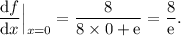
Finally:
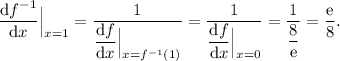
We can check the answer by finding the inverse:
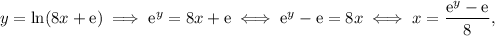
so that
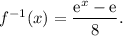
Therefore:
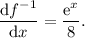
Which finally gives the same answer as before:
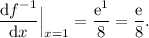
Answer: