Question

There is no charge at the upper terminal of the ele- ment in Fig. 1.5 for t 6 0. At t = 0 a current of 125e-2500t mA enters the upper terminal. a) Derive the expression for the charge that accu- mulates at the upper terminal for t 7 0. b) Find the total charge that accumulates at the upper terminal. c) If the current is stopped at t = 0.5 ms, how much charge has accumulated at the upper terminal?

Answer 1

A) The charge accumulated on upper plate for t>0 is

`q(t)=50[1-e^(-2500t)]\mu C`

B) The total charge that accumulates at the upper terminal is 50μC

C) If the current is stopped at t = 0.5 ms then total charge stored on upper terminal is 35.67μC

Step-by-step explanation:

Given that:

`I(t)=0 \quad \quad \quad \quad \quad t<0\\\\I(t)= 125e^(-2500t) \quad t\geq 0`

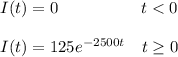
A) The charge that accumulates at the upper terminal for t > 0:

As we know

`q(t)=\int {I(t)} \, dt`

for t > 0

`q(t)=\int\limits^t_0 {I(t)} \, dt\\q(t)=\int\limits^t_0 {125e^(-2500t) mA} \, dt\\q(t)=(125* 10^(-3))[(e^(-2500t))/(-2500)]^(t)_(0)\\\\q(t)=( 50* 10^(-6))[-e^(-2500t)]^(t)_(0)\\\\q(t)=( 50* 10^(-6))[-e^(-2500t)+1]\\\\`

The charge accumulated on upper plate for t>0 is

`q(t)=50[1-e^(-2500t)]\mu C---(1)`

B) The total charge that accumulates at the upper terminal can be found by substituting t → ∞ in equation (1)

`q(t)=( 50* 10^(-6))[1-e^(-2500(\infty))]\\q(t)=(50* 10^(-6))[1-0]\\q(t) =50\mu C`

C) If the current is stopped at t = 0.5 ms then

`q(t)=( 50* 10^(-6))[1-e^{-2500(0.5*10^(-3))}]\\q(0.5ms)=35.67\mu C`