Answer:
A. Between 14 and 15.
Explanation:
Let x be the one leg of the right triangle.
We have been given that the legs of a right triangle are in the ratio of 3 to 1. So, the other leg of the right triangle would be 3x.
We are also told that the length of the hypotenuse of the triangle is √40.
Using Pythagoras theorem, we can set am equation as:
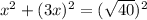
Let us solve for x.

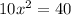
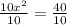

Take square root of both sides:


The other leg would be
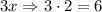 .
.
The perimeter of the triangle would be:
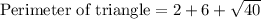
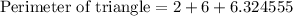

Therefore, the perimeter of the triangle is between 14 and 15 and option A is the correct choice.