Question

A flat plate is oriented parallel to a 45 m/s airflow at 20°C and atmospheric pressure. The plate is L = 1 m in the flow direction and 0.5 m wide. On one side of the plate, the boundary layer is tripped at the leading edge, and on the other side there is no tripping device. Find the total drag force on the plate.

Answer 1

4.192 N

Step-by-step explanation:

Step 1: Identify the given parameters

Velocity of airflow = 45m/s

air temperature = 20⁰

plate length and width = 1m and 0.5m respectively.

Step 2: calculate drag force due to shear stress,
`F_(s)`

`F_(s) = C_(f) (1)/(2) (\rho{U_(o)}WL)`

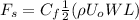
Note: The density and kinematic viscosity of air at 20⁰ at 1 atm, is 1.2 kg/m³ and 1.5 X 10⁻⁵ N.s/m²

⇒The Reynolds number (
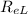`R_(eL)`) based on the length of the plate is

`R_(eL) =(VXL)/(U)`

`R_(eL) =(45X1)/(1.5 X 10^(-5))`

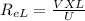
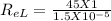
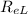`R_(eL)` = 3 X10⁶ (flow is turbulent, Re ≥ 500,000)

⇒The average shear stress coefficient (
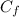`C_(f)`) on the "tripped" side of the plate is

`C_(f) = (0.074)/((R_(e))^(1)/(5))`

`C_(f) = (0.074)/((3 X10^6)^(1)/(5))`

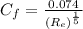
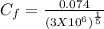
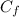`C_(f)` = 0.0038

⇒The average shear stress coefficient (
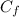`C_(f)`) on the "untripped" side of the plate is

`C_(f) = (0.523)/(in^2(0.06XR_(e))) -(1520)/(R_(e))`

`C_(f) = (0.523)/(in^2(0.06 X 3X10^6)) -(1520)/(3X10^6)`

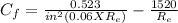
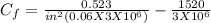
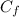`C_(f)` = 0.0031

The total drag force =
`(1)/(2)(1.2 X 45^2 X 1 X 0.5 (0.0038 +0.0031)`

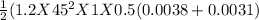
The total drag force is 4.192 N