Question

The side of the base of a square prism is increasing at a rate of 5 meters per second and the height of the prism as decreasing at a rate of 2 meters per second. At a certain instant, the base's side is 6 meters and the height is 7 meters. What is the rate of change of the volume of the prism at that instant fin cubic meters per second?

A. -348
B. 492
C. -492
D. 348

Answer 1

D. 348

Explanation:

The volume of the square prisma is given by the following formula:

`V = s^(2)h`

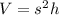
In which h is the height, and s is the side of the base.

Let's use implicit derivatives to solve this problem:

`(dV)/(dt) = 2sh(ds)/(dt) + s^(2)(dh)/(dt)`

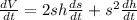
In this problem, we have that:

`(ds)/(dt) = 5, (dh)/(dt) = -2, h = 7, s = 6`

So

`(dV)/(dt) = 2sh(ds)/(dt) + s^(2)(dh)/(dt)`

`(dV)/(dt) = 2*6*7*5 + (6)^(2)*(-2) = 348`

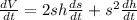
So the correct answer is:

D. 348