Answer:
D. 348
Explanation:
The volume of the square prisma is given by the following formula:
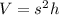
In which h is the height, and s is the side of the base.
Let's use implicit derivatives to solve this problem:
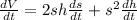
In this problem, we have that:
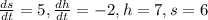
So
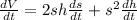
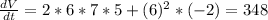
So the correct answer is:
D. 348