Question

A solid plate, with a thickness of 15 cm and a thermal conductivity of 80 W/m·K, is being cooled at the upper surface by air. The air temperature is 10°C, while the temperatures at the upper and lower surfaces of the plate are 650 50 and 60°C, respectively. Determine the convection heat transfer coefficient of air at the upper surface and discuss whether the value is reasonable or not for force convection of air.

Answer 1

To determine the convection heat transfer coefficient of air at the upper surface, we need to know the surface area of the plate which is not provided in the given question.

Step-by-step explanation:

The convection heat transfer coefficient of air at the upper surface can be determined using Newton's law of cooling. According to Newton's law of cooling, the rate of heat transfer through convection is directly proportional to the temperature difference between the solid surface and the surrounding fluid and the surface area of the solid.

Therefore, the heat transfer rate can be calculated using the formula:

Q = h * A * (Ts - T∞)

Where:

1. 
   
3. Q is the heat transfer rate
4. 
   
6. h is the convection heat transfer coefficient
7. 
   
9. A is the surface area of the solid
10. 
    
12. Ts is the temperature of the solid surface
13. 
    
15. T∞ is the temperature of the surrounding fluid

In this case, we are given the following values:

• 
  
• A = ?, Ts = 650°C, T∞ = 10°C
• 
  
• Q = ?
• 
  
• Thickness of the plate = 15 cm = 0.15 m
• 
  
• Thermal conductivity of the plate = 80 W/m·K

To find the surface area, we need to know the dimensions of the plate. Once we have the surface area, we can solve for the convection heat transfer coefficient using the given formula. However, the surface area is not provided in the question, so we cannot determine the convection heat transfer coefficient without that information.

Answer 2

To solve this problem we will use the two principles that are visible according to the phenomena described in the problem: Heat transfer by conductivity and Heat transfer by convection.

This thermal transfer will be equivalent and with it we can find the value asked.

Note: We will assume that the temperature value at the plate surface is: 60 ° C (For the given value of 650 50)

For Thermal Transfer by Conduction

`Q_(cn) = -kA (\Delta T)/(\Delta x)`

`Q_(cn) = -kA (T_1-T_2)/(L)`

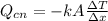
Where,

k = Thermal conductivity

A = Cross-sectional Area

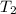`T_2` = Temperature of the bottom surface

`T_1`= Temperature of the top surface

L = Length

Replacing we have that

`Q_(cn) = -(80W\cdot K)(A)(50\°C-60\°C)/(15cm(1m)/(100cm))`

`Q_(cn) = 5333.33A`

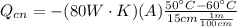
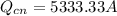
For Thermal Transfer by Convection

`Q_(cv) = hA(T_1-T_(\infty))`

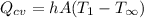
Where,

h = Convection heat transfer coefficient

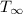`T_(\infty)`= Surrounding temperature

A = Surface Area

Replacing we have that

`Q_(cv) = hA(50\°C-10\°C)`

`Q_(cv) = 40hA`

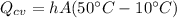
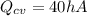
Since the rate of heat transfer by convection is equal to that given by conduction we have to:

`Q_(cn)=Q_(cv)`

`5333.33A = 40hA`

`h = 133.33W/m^2\cdot K`

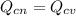
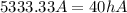
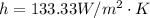
It is stated that the typical values of forced convection of gases lies in the range of
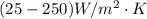`(25-250)W/m^2\cdot K`. The obtained value is reasonable for forced convection of air.