Question

A uniform disk, a uniform hoop, and a uniform solid sphere are released at the same time at the top of an inclined ramp. They all roll without slipping. In what order do they reach the bottom of the ramp?A uniform disk, a uniform hoop, and a uniform solid sphere are released at the same time at the top of an inclined ramp. They all roll without slipping. In what order do they reach the bottom of the ramp?hoop, sphere, diskhoop, disk, spheredisk, hoop, spheresphere, disk, hoopsphere, hoop, disk

Answer 1

The order in which a sphere, disk, and hoop reach the bottom of an incline when released from the same height is determined by their moments of inertia. The solid sphere arrives first, followed by the disk, and finally the hoop.

Step-by-step explanation:

In the scenario where a uniform disk, a uniform hoop, and a uniform solid sphere are released from the top of an inclined ramp and roll without slipping, the order in which they reach the bottom depends on their moments of inertia and the distribution of mass. The solid sphere has the smallest moment of inertia relative to its mass (I = 2/5 MR²), which means it will accelerate faster than the other shapes and hence get to the bottom first. The uniform disk, with a moment of inertia of I = 1/2 MR², will follow. The uniform hoop has the largest moment of inertia (I = MR²) for a given mass and radius, so it will accelerate the slowest of the three and reach the bottom last.

Therefore, the objects reach the bottom of the ramp in the following order: sphere, disk, hoop.

Answer 2

First let's write down the moment of inertia of the objects.

`I_(sphere) = (2)/(5)mR^2\\I_(disk) = (1)/(2)mR^2\\I_(hoop) = mR^2`

If they all roll without slipping, then the following relation is applied to all ot them:

`v = \omega R`

where v is the translational velocity and ω is the rotational velocity.

We will use the conservation of energy, because we know that their initial potential energies are the same. (Here, I will assume that all the objects have the same mass and radius. Otherwise we couldn't determine the difference. )

`K_1 + U_1 = K_2 + U_2\\0 + mgh = (1)/(2)I\omega^2 + (1)/(2)mv^2`

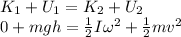
For sphere:

`(1)/(2)(2)/(5)mR^2((v)/(R))^2 + (1)/(2)mv^2 = mgh\\(1)/(5)mv^2 + (1)/(2)mv^2 = mgh\\(7)/(10)mv^2 = mgh\\v_(sphere) = \sqrt{(10gh)/(7)}`

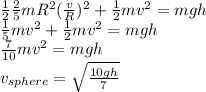
For disk:

`(1)/(2)(1)/(2)mR^2((v)/(R))^2 + (1)/(2)mv^2 = mgh\\(1)/(4)mv^2 + (1)/(2)mv^2 = mgh\\(3)/(4)mv^2 = mgh\\v_(disk) = \sqrt{(4gh)/(3)}`

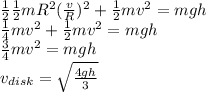
For hoop:

`(1)/(2)mR^2((v)/(R))^2 + (1)/(2)mv^2 = mgh\\(1)/(2)mv^2 + (1)/(2)mv^2 = mgh\\mv^2 = mgh\\v_(hoop)= √(gh)`

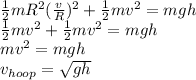
The sphere has the highest velocity, so it arrives the bottom first. Then the disk, and the hoop arrives the last.

Step-by-step explanation:

The moment of inertia can be defined as the resistance to the rotation. If an object has a high moment of inertia, it resist to rotate more so its angular velocity would be lower. In the case of rolling without slipping, the angular velocity and the linear (translational) velocity are related by the radius, so the object with the highest moment of inertia would arrive the bottom the last.